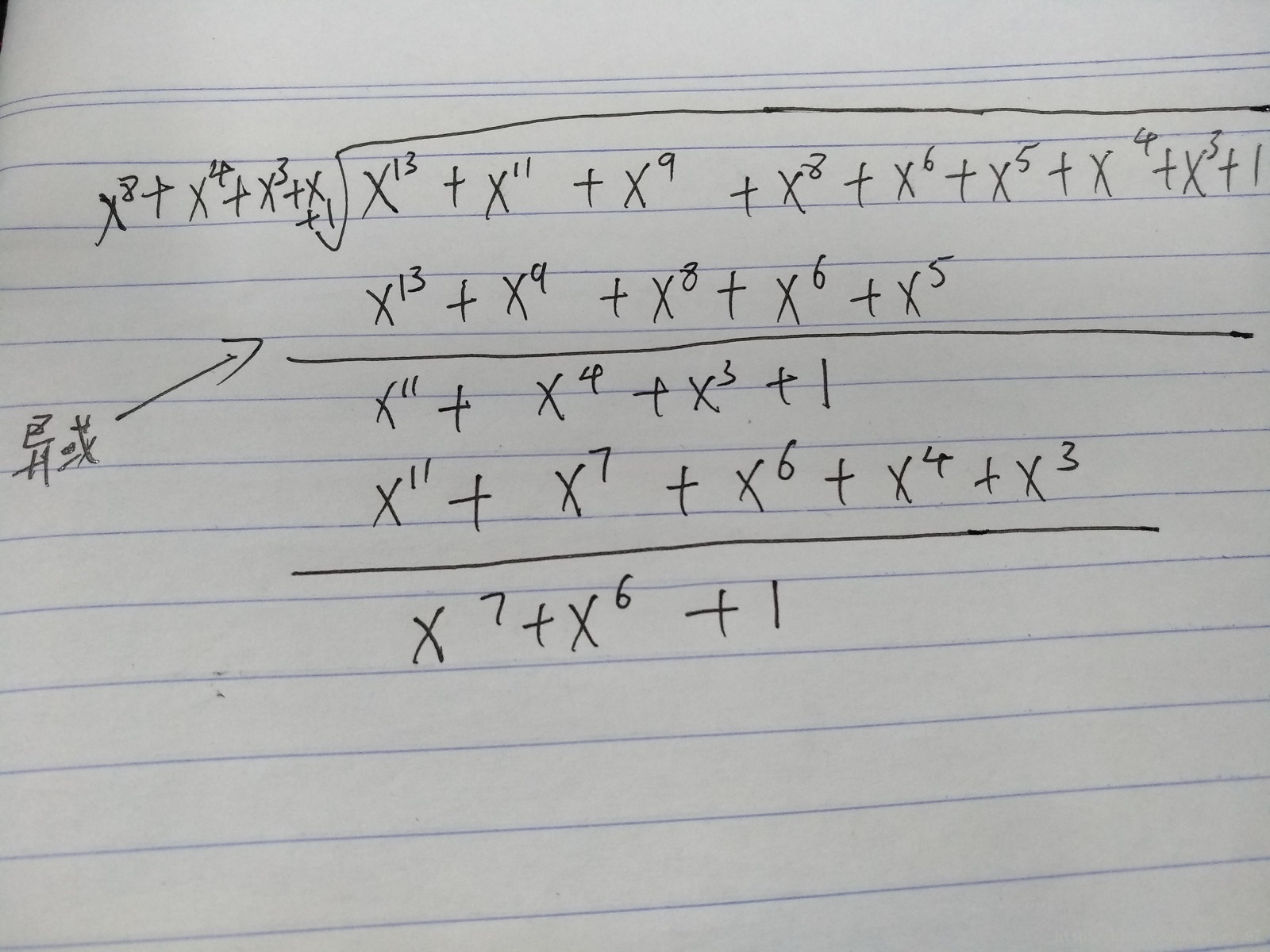JB哥の密码学期末复习2.0

题型

判断题2（分）*5（小题），
简答题5（分）*5（6题），
计算题10（分）*4（小题）,
论述题1题，20分

重点详解

第1章引言

清楚信息安全专业学习密码学的原因

解决信息安全的三个基本安全需求：
- 信息的机密性保证
- 信息的真实性认证
- 承诺的不可否认性保证

第2章流密码

简答：掌握流密码的基本思想

流密码的基本思想是利用密钥k产生一个密钥流z=z₀z₁….，并使用如下规则对明文串x=x₀x₁x₂….加密：

y=y₀y₁y₂…..=E(x₀)E(x₁)E(x₂)…..

密钥流由密钥流发生器f产生：
z_i=f(k,σ_i)
这里σ_i是加密器中的记忆元件（存储器）在i时刻的状态，f是由密钥k和σ_i产生的函数。

第3章分组密码

简答：理解分组密码的CBC工作模式，能够画出该模式的加解密示意图

CBC工作模式，一次对一个明文分组加密，每次加密使用同一密钥，加密算法的输入是当前明文分组和前一密文分组的异或，因此加密算法的输入不会显示出与这次的明文分组之间的固定关系，所以重复的明文分组不会在密文中暴露出这种重复关系。
由于CBC模式的链接机制，CBC模式对加密长于64比特的消息非常合适。
CBC模式除能够获得保密性外，还能用于认证。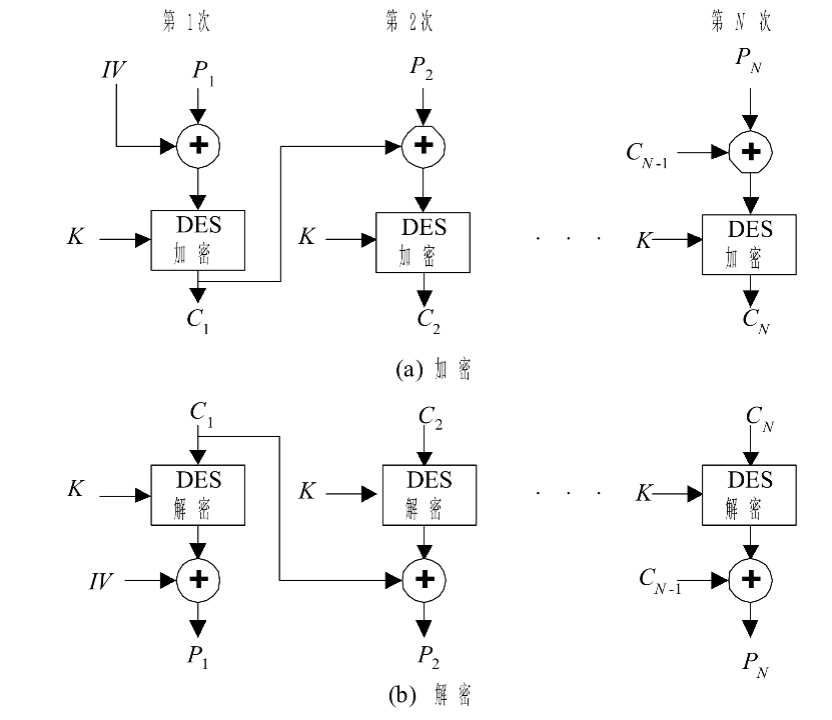

字节代替变换详解

有限域GF(2⁸)

基本概念

可以把出b₇b₆b₅b₄b₃b₂b₁b₀构成的一个字节看成是系数在(0, 1)中取值的多项式：
b₇x⁷+b₆x⁶+b₅x⁵+b₄x⁴+b₃x³+b₂x²+b₁x+b₀
如{57}（01010111）可写成： x⁶ + x⁴ + x² + x + 1

多项式加法

在多项式表示中，两个元素的和是一个多项式，其系数是两个元素的对应系数的模2加(即异或)。
例题如下：
例如：“57”和“83”的和为： 57+83＝D4，
或者采用其多项式记法：
57→01010111 → x⁶ + x⁴ + x² + x + 1
83 →10000011 → x⁷+x+1
(x⁶ + x⁴ + x² + x + 1)+(x⁷+x+1)＝x⁷+x⁶+x⁴+x² →11010100 →D4

显然，该加法与简单的以字节为单位的比特异或是一致的。

多项式乘法

直接给图

注意：

x⁷和自身相加，相当于与自己异或，所以为0.
多项式取模是异或运算，不是除法运算，如图

字节代替变换

先将该字节A变换为有限域GF(2)中的乘法逆元素T。
T= A^-1 mod m(x)
m(x) = x⁸+x⁴+x³+x+1
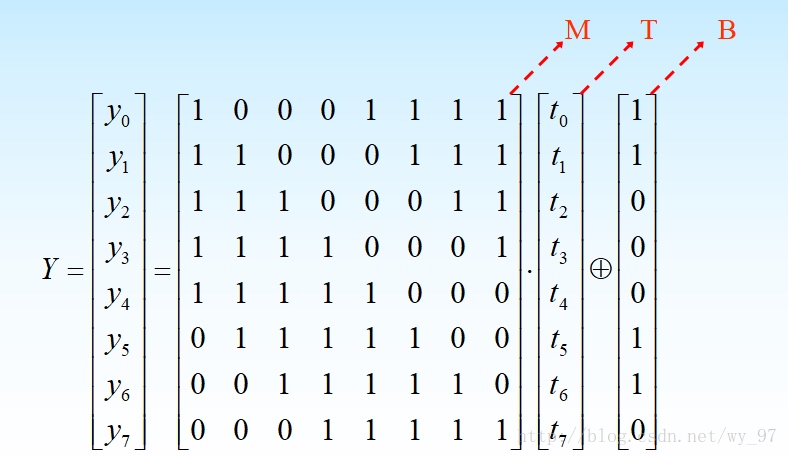
即 A·T ≡T·A ≡ 1 mod m(x)
对X作GF(2)上的仿射变换： Y = M · T ⊕ B

第4章公钥密码

RSA算法的加密与解密计算

算法描述

选择两个大素数 p，q，（p，q为互异素数，需要保密）
计算
- n = p x q
- φ(n) = (p-1) * (q-1)
- 选择与φ(n) 互素的整数e
- 根据e * d ≡ 1 mod φ(n)计算出d
- 得到公钥{e , n} 私钥{d , n}
加密： C = M^e mod n
脱密： M = C^d mod n

第5章数字签名

ElGamal数字签名体制

准备一个大素数p 和乘法群生成元g
在1～p-2范围内选择x
计算y=g^xmod p,x为私钥，y p g公开
设m∈Z是待签名的消息，秘密随机选取一个整数k，1≤k≤p-2，且(k,p-1)=1，计算
- r=g^k mod p
- s=k^-1 (m-rx)(mod p-1)
- 则(m,r,s)为对消息m的数字签名
对方收到对消息m的数字签名(m,r,s)后，利用签名者的公开密钥y,g,p可对签名进行以下验证：
- y^rr^s=g^m (mod p)
如果上式成立，则接受该签名，否则拒绝该签名。

第6章哈希函数

第8章密钥分配与管理

D-H密钥交换协议

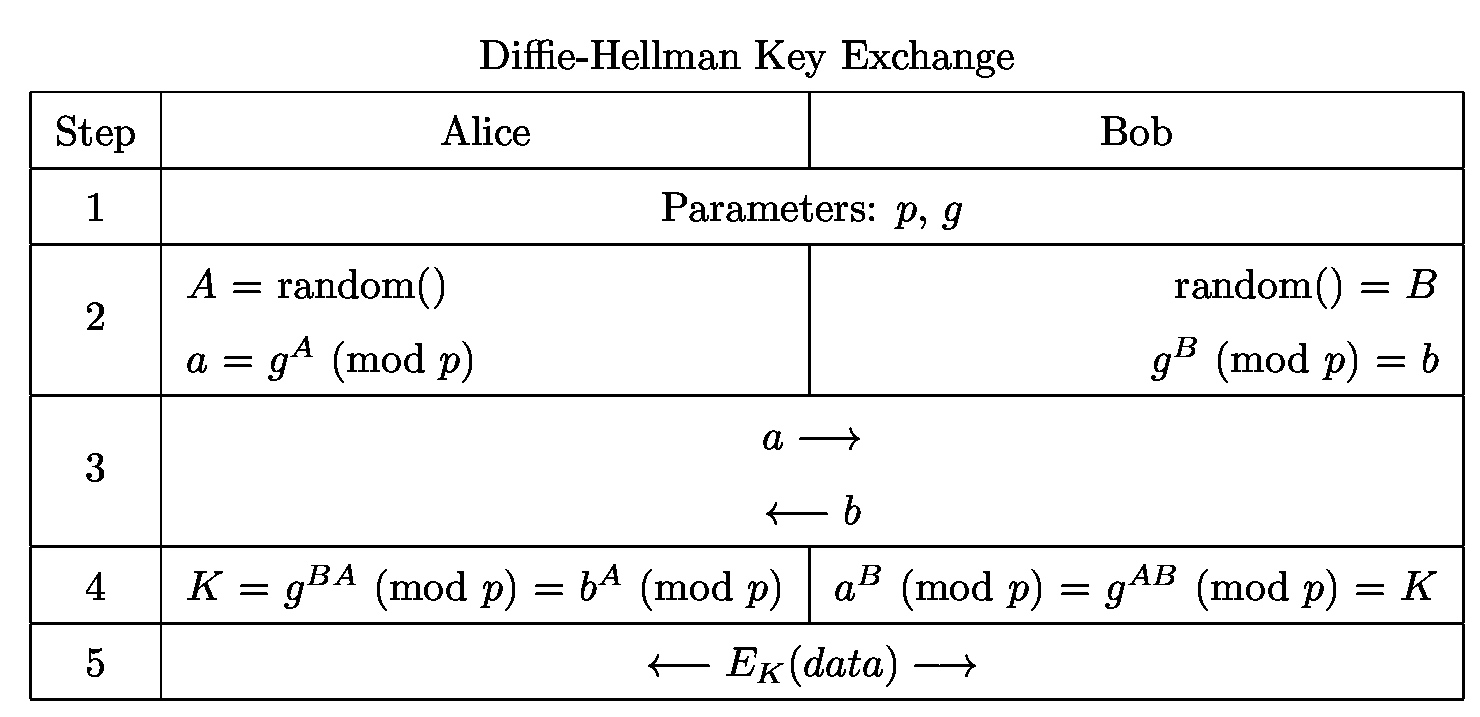
例题

第11章密码学新方向

5种密码学新方向或新技术

身份基密码体制
属性基加密体制
全同态加密方案
后量子密码学（基于Hash的签名体制、基于纠错码的公钥密码学、基于格的公钥密码学、多变量公钥密码学）
可搜索加密
时间控制加密

综合问题

介绍一种密码学协议研究与应用动态。
提出一种安全应用场景，试设计出相应的密码协议实现安全应用。
介绍一种安全应用场景，分析该安全场景应用了哪些密码技术，并简述如何保障了安全性。

私人回答，你看个锤子。